Ajuca
AJUCA necesita la publicidad para costear hosting y el dominio. Por favor considera deshabilitar tu AdBlock en nuestro sitio. También puedes hacernos una donación entrando en linuxparty.es, en la columna de la derecha.
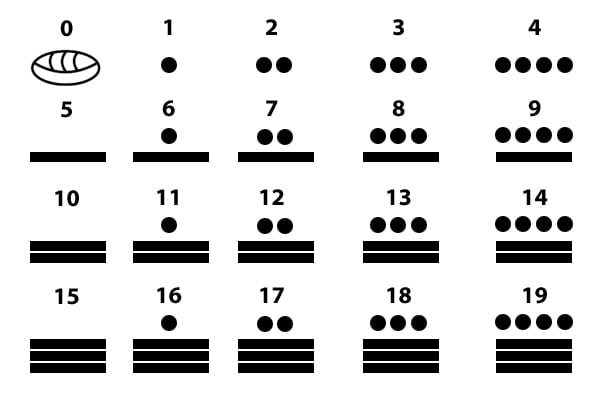
Los trabajos astronómicos de los mayas los llevaron a desarrollar un complejo sistema de numeración en el que también se descubrió el cero. Te explicamos cómo funciona.
Entre las peculiaridades de la civilización maya se encuentra su sistema de numeración. Dicho sistema posee una base vigesimal de raíz mixta. Es decir, la contabilidad de los números se distribuye teniendo como base el número veinte y la raíz cambia de un lugar a otro.
Lee: La limpia con huevos y refresco que cura el espíritu en Chiapas
Además, otra de sus principales características es el desarrollo del número y concepto cero de una forma autónoma. Este complejo sistema fue desarrollado durante la época preclásica, aproximadamente en el año 36 a.C.
Leer más: Los números mayas, son una maravilla matemática Escribir un comentario
¿Qué es un vatio, un voltio o un amperio? Unidades de medida eléctricas que, en ocasiones, se confunden. Veamos qué mide cada una de ellas y su definición.
Veamos brevemente estas tres unidades eléctricas básicas para poder comprender otras unidades como las que suelen venir en la factura de la luz.
Voltios o Voltaje: ¿Qué es un voltio?
El voltio o volt en inglés, cuyo símbolo es V, es la unidad derivada del Sistema Internacional para el potencial eléctrico, la fuerza electromotriz y la tensión eléctrica. Recibe su nombre en honor a Alessandro Volta, quien en 1800 inventó la pila voltaica, la primera batería química.
«Ni la matemática ni la física moderna existirían sin el álgebra. » «El lenguaje de la ciencia moderna todavía tiene muchas referencias a sus raíces árabes», señaló en el programa.
«Muchas de las ideas que anteriormente se pensaba que habían sido conceptos nuevos y brillantes gracias a los matemáticos europeos de los siglos XVI, XVII y XVIII, ahora se sabe que fueron desarrolladas por matemáticos árabes/islámicos unos cuatro siglos antes», escribieron John Joshep O'Connor y Edmund Frederick Robertson, de la Universidad St. «En muchos aspectos, las matemáticas que se estudian hoy tienen un estilo mucho más cercano al de la contribución árabe/islámica que a la de los griegos».
Un matemático australiano ha descubierto lo que puede ser el ejemplo más antiguo conocido de geometría aplicada, en una tablilla de arcilla babilónica de 3.700 años de antigüedad. Conocida como Si.427, la tableta tiene un plano de campo que mide los límites de algunas tierras.
La Tablilla de está grabada con un “plano de campo notablemente preciso” siendo el ejemplo más antiguo conocido de geometría aplicada en el mundo.
Del informe: La tableta data del período babilónico antiguo entre 1900 y 1600 a. C. y fue descubierta a fines del siglo XIX en lo que hoy es Irak. Se había alojado en el Museo Arqueológico de Estambul antes de que el Dr. Daniel Mansfield de la Universidad de Nueva Gales del Sur lo rastreara. Mansfield y Norman Wildberger, profesor asociado de la UNSW, habían identificado previamente otra tableta babilónica que contenía la tabla trigonométrica más antigua y precisa del mundo.
En ese momento, especularon que era probable que la tableta hubiera tenido algún uso práctico, posiblemente en topografía o construcción. Esa tablilla, Plimpton 322, describía triángulos en ángulo recto usando triples pitagóricos: tres números enteros en los que la suma de los cuadrados de los dos primeros es igual al cuadrado del tercero, por ejemplo, 3^2 + 4^2 = 5^2. /// También representada como: 3² + 4² = 5²
Este video explicativo le ayudará a resolver sus dudas sobre la integración por fracciones parciales.
En esta serie de dos videos se explica de forma extremadamente fácil qué es una integral y cómo funciona dicha integral y como se representa.
El vídeo es también, extramadamente ameno. Os lo recomiendo.
Desde hace algunos meses, el buscador de Google nos ofrece la posibilidad de realizar representaciones gráficas de funciones matemáticas, incluso realizando gráficas tridimensionales. Gracias a este tipo de funcionalidades y a que, con cada vez mayor frecuencia, recurrimos a la red para buscar información de apoyo y consultar fuentes bibliográficas, no nos resulta raro encontrar en una mesa de estudio un ordenador. Al igual que podemos complementar las funciones de nuestro navegador, por ejemplo, para hacerlo más social y hacernos más fácil conectar con nuestros amigos a través de Twitter o Facebook, también podemos personalizar nuestro navegador y convertirlo en una potente herramienta de estudio que nos ayude a preparar los exámenes finales.
Los investigadores con la esperanza de obtener '2' como respuesta a una prueba tan buscada en la participación de números primos, están celebrando el hecho de que un matemático ha luchado por averiguar que un número infinito de números primos están separados por 70 millones. Esa meta es la prueba de una conjetura. Los números primos "Primes" abundan entre los números más pequeños, pero son cada vez son menos frecuentes, a medida que uno va hacia un mayor número, pero existen excepciones.. los "primos gemelos", que son pares de números primos que difieren en el valor 2. La conjetura "prima gemela" dice que existe un número infinito de tales pares de gemelos. Algunos atribuyen la conjetura al matemático griego Euclides de Alejandría, lo que lo convierte en uno de los más antiguos problemas abiertos en matemática.
Un nuevo estudio publicado en la American Mathematical Society, mirando los datos de 86 países, para probar la hipótesis mayor de variabilidad masculina como la principal razón de la escasez de mujeres destacadas en matemáticas. Concluye que los factores son los culturales y no biológicos PDF) los que hacen que las diferencias en habilidades matemáticas entre hombres y mujeres.
Esta entrada del blog del Washington Post, "trata sobre la Evaluación Nacional del Progreso Educativo en la prueba en concreto, la parte de matemáticas). Uno de los miembros del consejo escolar fueron incapaces de responder a cualquiera de las 60 preguntas de matemáticas, aunque acertó 10 de ellos. Luego pasa a afirmar que las matemáticas no son relevantes para muchas personas... Si quieres sentirte como Einstein, echa un vistazo a algunos ejemplos de preguntas. "Tal vez a esto se refieren principalmente al tipo de habilidades para la vida que son suficientes para tener éxito en la gestión.
-
Matemáticas
- 3 grandes matemáticos árabes y sus grandes aportaciones a la ciencia
- Los números mayas, son una maravilla matemática
- Qué es un Amperio, un voltio y un vatio
- Matemático australiano descubre geometría aplicada grabada en tablilla de 3.700 años
- Matemáticas, Integración por Fracciones Parciales
- [VIDEO] Fácil de Entender, Representación gráfica de una INTEGRAL.
- Estudia matemáticas con Google Chrome
- Mayor avance en Matemáticas sobre números primos.
- Nuevo estudio concluye que la brecha de género en Mates es Cultural, no es biológica, sino cultural
- ¿Es usted mejor en matemáticas que un chico de cuarto o 10) Grado?
- La copa de Pitágoras
- Aprender de mecánica y autovectores rompiendo tizas
- Dibujar raices cuadradas
- La cascada infinita de Escher existe en el mundo real
- ¿Cuantos litros tiene un barril de petroleo?
|
|
 |
 |
 |
Suscriberse a Newsletter
Buscar
¿Quien está online?
Hay 128 invitados y ningún miembro en línea
Últimos Comentarios
- ¿Windows 7 es una copia de KDE? (1)
- El Arca de la Alianza (2)
- 10 plantas que purifican el aire de tu casa (2)
- Es devuelta o de vuelta? (1)
- En 2.5 minutos ingenieros mexicanos potabilizan agua residual y de mar (1)
- El enorme cometa 67P de la sonda Rosetta, comparado con una ciudad (1)
- Pallet House: como costruirse una casa ecológica por menos de 100€ (1)
- Esta es la primera pistola de metal creada con una impresora 3D (2)
- Cañaveral ha perdido al ilustre paisano: José María Hercilla Trilla (1)
- Fedora 14, añade un nuevo sabor picante a Linux. (1)
Filtro de Categorías
Contenido más leido
- Es devuelta o de vuelta?
- Un simulador de trenes GRATUITO
- Las Chicas Virtuales más guapas.
- Tribunal Supremo UK implica el Copyright a los Titulares – ¿Pronto los links?
- Localizador de Teléfonos Móviles.
- Cementerio de camiones gigantes
- Contruye tu propio motor magnético.
- Foto del día: Azafata de Ryanair de día y pornostar de noche
- Lara Croft Desnuda!
- Contratar publicidad con Ajuca
- Elsa Pataky, desnuda en Interviú
- Ceremonia de circuncisión femenina
- El cuento de la Cigarra y la Hormiga y su Actualización a la Española. [Humor]
- Generador español de insultos
- Un ‘Marina D’Or’ en Extremadura